Lernauftrag 11: Logische Grundschaltungen analysieren
Hier findest du die Aufgaben ohne Lösungen.
Von den folgenden acht Schaltungen besitzen jeweils zwei das gleiche logische Verhalten.
Aufgabe 1
Erstelle zu den Schaltungen A, B, C und D die Funktionsgleichungen.
Aufgabe 2
Erstelle zu allen acht Schaltungen die Wertetabellen.
Aufgabe 3
Benenne die Schaltungen mit gleichem logischen Verhalten.
A)
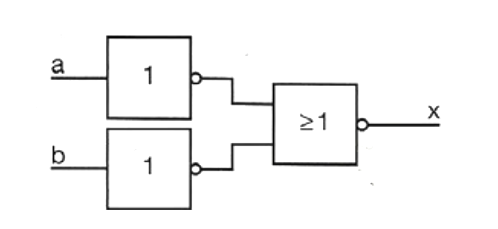
\(x=\overline a \overline\lor \overline b=\overline{(\overline a\lor \overline b)}\)
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
B)
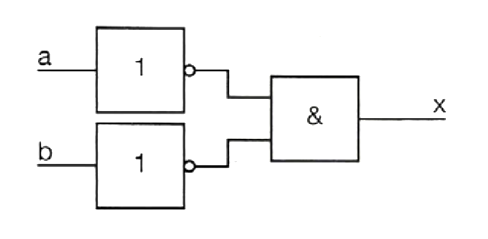
\(x=\overline a\land\overline b\)
| b | a | x |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
C)
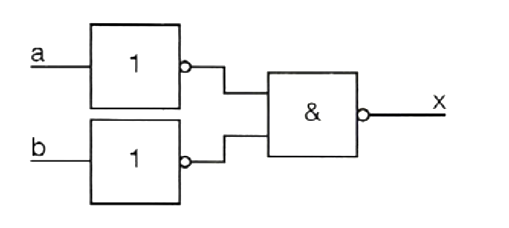
\(x=\overline a\overline\land\overline b=\overline{(\overline a\land \overline b)}\)
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
D)
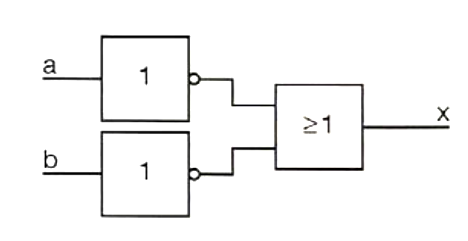
\(x=\overline a \lor \overline b\)
| b | a | x |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
E)
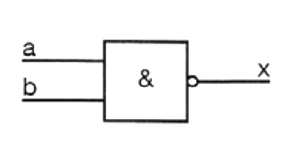
| b | a | x |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
F)
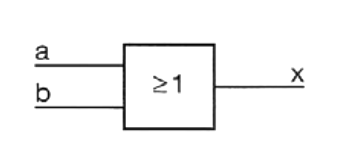
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
G)
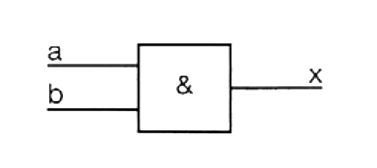
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
H)
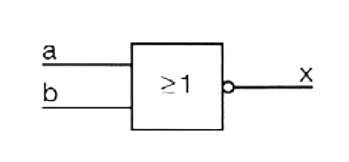
| b | a | x |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
E=D
F=C
B=H
G=A
Aufgabe 4
Vereinfache die Verknüpfungsschaltung.
Hinweise: Wertetabelle erstellen, Vereinfachungen zeichnen
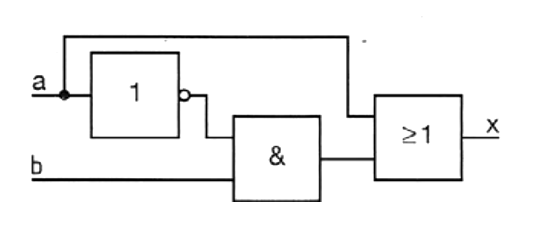
Wertetabelle:
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Vereinfachung:

Aufgabe 5
Vereinfache die Verknüpfungsschaltung.
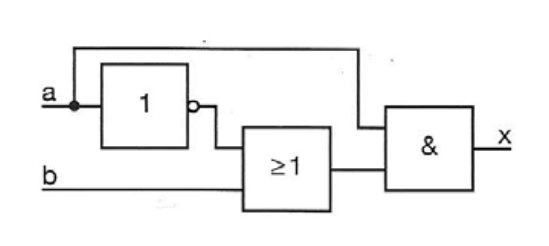
Wertetabelle:
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Vereinfachung:

Aufgabe 6
Stelle für die Analyse der Schaltung
- die Wertetabelle auf,
- zeichne den Signal-Zeit-Verlauf des Ausgangssignals
- stelle die Funktionsgleichung auf
- beschreibe die Besonderheiten der Schaltung
- gib das Logiksymbol an
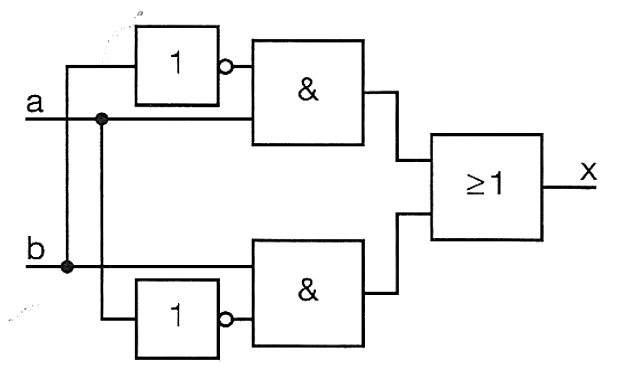
Wertetabelle:
| b | a | x |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Funktionsgleichung:
Exklusiv-ODER / XOR / Antivalenz
\(x=a\nleftrightarrow b=(a\land \overline b)\lor(\overline a\land b)\)
Logiksymbol: Siehe Tabellenbuch S. 355
Besonderheit:
Das Ergebnis x ist genau dann 1, wenn die Eingangssignale unterschiedlich sind.
Das Ergebnis \(x\) ist genau dann 0, wenn beide Eingangssignale identisch sind.
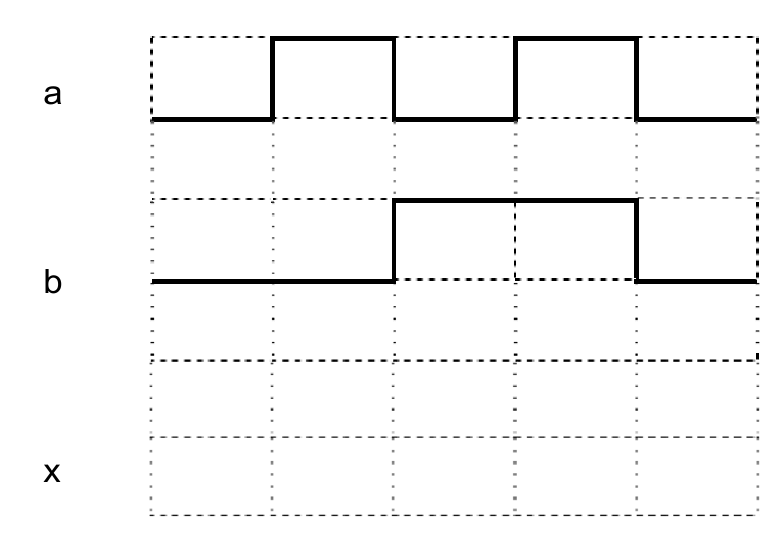
Zeitquadrant 1: \(a = 0, b = 0 \Rightarrow x=0\)
Zeitquadrant 2: \(a = 1, b = 0 \Rightarrow x=1\)
Zeitquadrant 3: \(a = 0, b = 1 \Rightarrow x=1\)
Zeitquadrant 4: \(a = 1, b = 1 \Rightarrow x=0\)
Zeitquadrant 5: \(a = 0, b = 0 \Rightarrow x=0\)
Aufgabe 7
Stelle für die Analyse der Schaltung
- die Wertetabelle auf,
- zeichne den Signal-Zeit-Verlauf des Ausgangssignals
- stelle die Funktionsgleichung auf
- beschreibe die Besonderheiten der Schaltung
- gib das Logiksymbol an
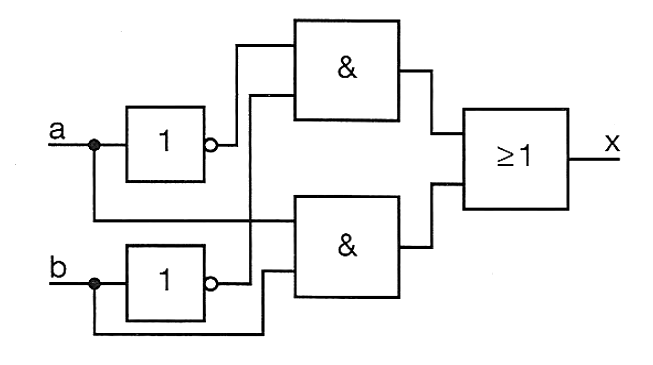
Wertetabelle:
| b | a | x |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Funktionsgleichung:
Exklusiv-NICHT-ODER / XNOR / Äquivalenz
\(x=a\leftrightarrow b=(a\land b)\lor(\overline a\land\overline b)\)
Logiksymbol: Siehe Tabellenbuch S. 355
Besonderheit:
Das Ergebnis \(x\) ist genau dann 1, wenn beide Eingangssignale identisch sind.
Das Ergebnis x ist genau dann 0, wenn die Eingangssignale unterschiedlich sind.

Zeitquadrant 1: \(a = 0, b = 0 \Rightarrow x=1\)
Zeitquadrant 2: \(a = 1, b = 0 \Rightarrow x=0\)
Zeitquadrant 3: \(a = 0, b = 1 \Rightarrow x=0\)
Zeitquadrant 4: \(a = 1, b = 1 \Rightarrow x=1\)
Zeitquadrant 5: \(a = 0, b = 0 \Rightarrow x=1\)
Weiter zur nächsten Lernaufgabe